四人追逐游戏 – Bowen Qin

游戏的设定是四个人A，B，C，D站在四个角，A追B，B追C，C追D，D追A。高数里面好像经常有类似的题目，今天用代码来模拟一下。

library(tidyverse)

dt_list <- list(
  tibble(
    name = c("A", "B", "C", "D"),
    x = c(1, 1, -1, -1),
    y = c(1, -1, -1, 1),
    direction = c(2, 3, 4, 1),
    n = 0
  )
)

生成一个tibble，其中

name列表示四个人的名字。
x、y是坐标。
direction列表示追逐的人的行号，比如A追B，B在第二行，所以A对应的direction是2。
n表示跑了几步，目前没有开始追，所以是0步。

# 设置程序最多跑5000步，防止程序出错而不收敛
N <- 5000   
# 设置每一步的步长
step_length <- 0.01

# 开始循环
for (i in 1:N) {
  dt = dt_list[[i]]
  x_diff = max(dt$x) - min(dt$x)
  y_diff = max(dt$y) - min(dt$y)
  # 因为x,y是浮点数，最终可能每个点的x,y都十分接近但不相等，因此用near()来判断
  if (!all(near(c(x_diff, y_diff), 0))) {
    dt_list[[i + 1]] <- dt %>% 
      # 每个人向所追的方向迈一步
      mutate(x_d = as_vector(dt[direction, "x"] - x),
             y_d = as_vector(dt[direction, "y"] - y),
             x = x + x_d * step_length,
             y = y + y_d * step_length,
             n = i)
  } else {
    break
  }
}

整理一下结果

dt <- do.call(bind_rows, dt_list)
dt

# A tibble: 7,572 × 7
   name       x      y direction     n     x_d     y_d
   <chr>  <dbl>  <dbl>     <dbl> <dbl>   <dbl>   <dbl>
 1 A      1      1             2     0 NA      NA     
 2 B      1     -1             3     0 NA      NA     
 3 C     -1     -1             4     0 NA      NA     
 4 D     -1      1             1     0 NA      NA     
 5 A      1      0.98          2     1  0      -2     
 6 B      0.98  -1             3     1 -2       0     
 7 C     -1     -0.98          4     1  0       2     
 8 D     -0.98   1             1     1  2       0     
 9 A      1.00   0.960         2     2 -0.0200 -1.98  
10 B      0.960 -1.00          3     2 -1.98    0.0200
# ℹ 7,562 more rows

dt %>% 
  slice_max(n)

# A tibble: 4 × 7
  name         x        y direction     n      x_d      y_d
  <chr>    <dbl>    <dbl>     <dbl> <dbl>    <dbl>    <dbl>
1 A      7.44e-9  4.30e-9         2  1892 -3.05e-9 -1.19e-8
2 B      4.30e-9 -7.44e-9         3  1892 -1.19e-8  3.05e-9
3 C     -7.44e-9 -4.30e-9         4  1892  3.05e-9  1.19e-8
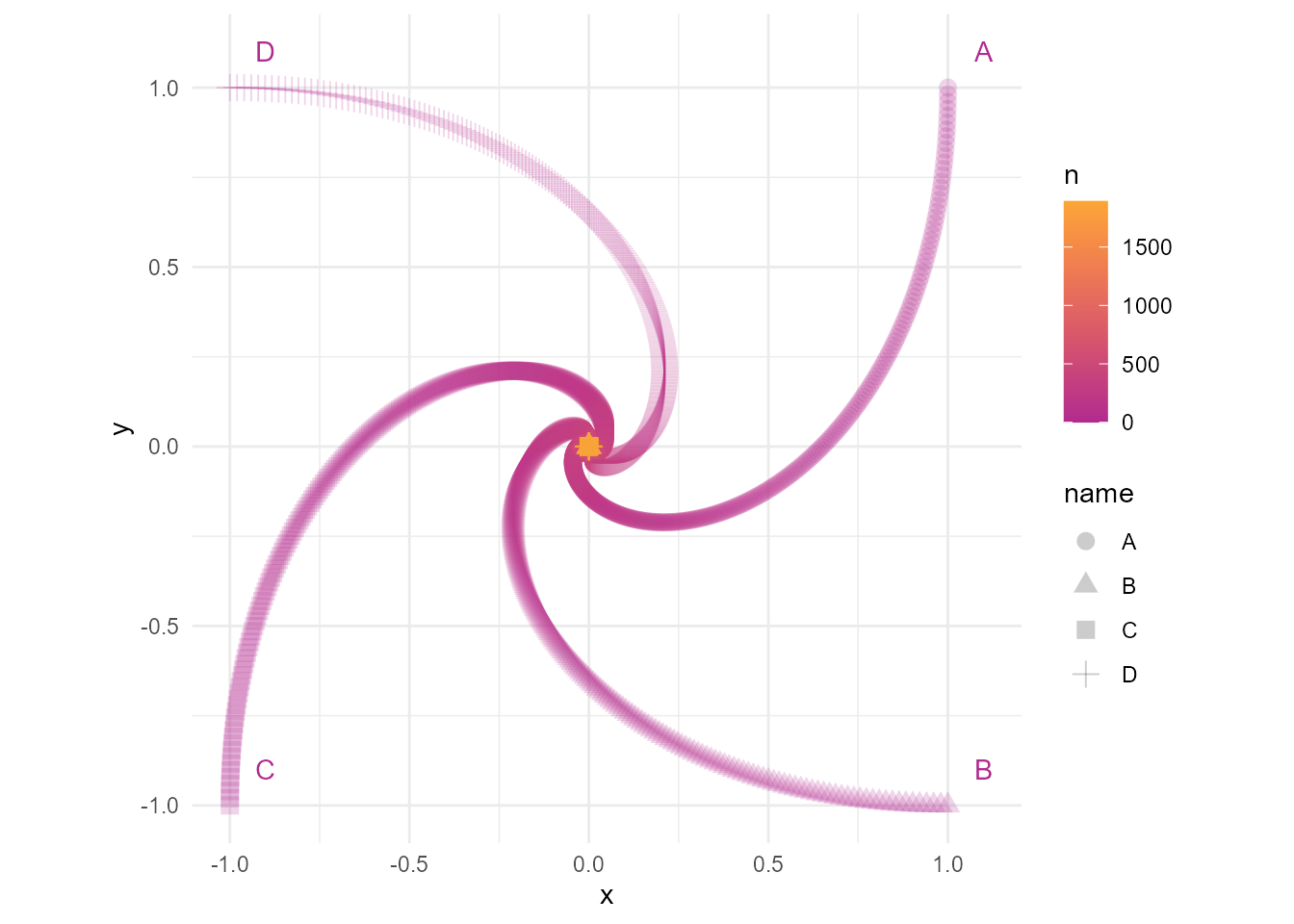
4 D     -4.30e-9  7.44e-9         1  1892  1.19e-8 -3.05e-9

达到收敛的状态花了1892步，即在步长为0.01时，1892步后四人追到彼此。

看下四个人的轨迹

dt %>% 
  ggplot(aes(x, y, color = n, pch = name)) +
  geom_point(alpha = 0.2, size = 3) +
  geom_text(data = dt_list[[1]],
            aes(x, y, label = name),
            nudge_x = 0.1,
            nudge_y = 0.1) +
  coord_equal() +
  scale_color_viridis_c(option = "C", end = 0.8, begin = 0.4) +
  theme_minimal()